일시 : 2022-11-10 23:54
Title : 재료의 강도
Memo
1. 응력-변형률 선도
기계적 성질
- 인장, 압축, 굽힘하중 등과 같은 외력에 대하여 재료가 저항하는 성질
- 인장강도, 항복강도, 굽힘강도, 비틀림강도, 경도
공칭응력
- 일반적으로 인중하중을 가하면 단면적이 감소하지만 이 감소량이 아주 작으므로 하중 P를 처음 단면적 A으로 나눈 응력
-
\[\Large \sigma = {P\over A_0}\]
진응력(실제응력)
- 하중에 의해 변형된 상태의 단면적 A’으로부터 구한 응력
-
\[\Large \sigma_t = {P\over A'}\]
응력-변형률 선도
- 비례한도 → 탄성한도 → 상항복점 → 하항복점 → 인장강도
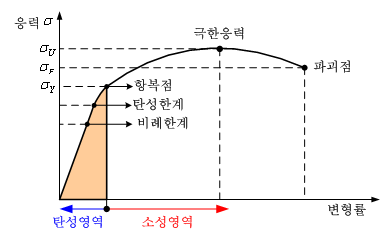
OB 구간
CD 구간
DF 구간
FG 구간
인장강도(극한강도)
-
\[\Large \sigma_{\mu} = {P_{max}\over A_0}={가해진최대외력\over 최초단면적}\]
2. 열응력
온도 변화에 의한 최종 길이(L₁)
-
\[\Large L_1 = L_0\bigg(1+\alpha(T_2-T_1) \bigg)\]
온도 변화에 의해 변화한 길이(λ)와 변형률(ε)
-
\[\Large \epsilon = \alpha(T_2-T_1)\]
열응력
-
\[\Large \sigma = E\epsilon = -E \alpha \Delta T = -E \alpha (T_2-T_1)\]
막대 고정부에서 발생하는 힘(F)
-
\[\Large F = \sigma A = AE \alpha(T_2-T_1)\]
- E = 탄성계수, ε = 변형률, α = 열(선)팽창계수, T₂ = 나중온도, T₁ = 처음온도
-
\[\Large \sigma = E\epsilon = -E\times \alpha \times \Delta T = -E \times \alpha \times (T_2-T_1)\]
3. 피로
-
\[\Large \sigma_a{\rm (응력진폭or교번응력)} = {\sigma_{max}-\sigma_{min}\over 2}\]
-
\[\Large \sigma_m{\rm (평균응력)} = {\sigma_{max}+\sigma_{min}\over 2}\]
S-N 선도

Source & Link
Be Connected Document
Serise
Keywords
Backup
- ˚C = 도씨
- G = 지, G’ = 지다시 or 지프라임
연결된 노트

